ベクトル化

最終更新日：2024-11-22 | ページの編集

概要

質問

  • ベクトルのすべての要素に一度に操作を行うにはどうすればよいですか？

目的

  • Rにおけるベクトル化された操作を理解する。

Rの関数のほとんどはベクトル化されており、ループを使用して各要素に対して1つずつ処理を行う必要なく、ベクトルのすべての要素に対して操作を実行します。 これにより、コードが簡潔で読みやすく、エラーが少なくなります。

R 

x <- 1:4
x * 2

出力 

[1] 2 4 6 8

乗算がベクトルの各要素に対して行われました。

2つのベクトルを加えることもできます：

R 

y <- 6:9
x + y

出力 

[1]  7  9 11 13

x の各要素が対応する y の要素と加算されました：

R 

x:  1  2  3  4
    +  +  +  +
y:  6  7  8  9
---------------
    7  9 11 13

次に、ループを使用して2つのベクトルを加算する方法を示します：

R 

output_vector <- c()
for (i in 1:4) {
  output_vector[i] <- x[i] + y[i]
}
output_vector

出力 

[1]  7  9 11 13

ベクトル化された操作を使用した出力と比較してください。

R 

sum_xy <- x + y
sum_xy

出力 

[1]  7  9 11 13

チャレンジ 1

gapminder データセットの pop 列を使用してみましょう。

gapminder データフレームに新しい列を作成し、 人口を100万人単位で表示してください。 データフレームの先頭または末尾を確認して、正しく動作したか確認してください。

gapminder データセットの pop 列を使用してみましょう。

gapminder データフレームに新しい列を作成し、 人口を100万人単位で表示してください。 データフレームの先頭または末尾を確認して、正しく動作したか確認してください。

R 

gapminder$pop_millions <- gapminder$pop / 1e6
head(gapminder)

出力 

      country year      pop continent lifeExp gdpPercap pop_millions
1 Afghanistan 1952  8425333      Asia  28.801  779.4453     8.425333
2 Afghanistan 1957  9240934      Asia  30.332  820.8530     9.240934
3 Afghanistan 1962 10267083      Asia  31.997  853.1007    10.267083
4 Afghanistan 1967 11537966      Asia  34.020  836.1971    11.537966
5 Afghanistan 1972 13079460      Asia  36.088  739.9811    13.079460
6 Afghanistan 1977 14880372      Asia  38.438  786.1134    14.880372

チャレンジ 2

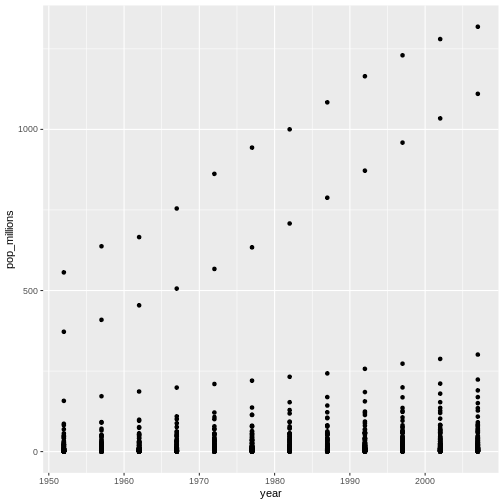
単一のグラフ上で、すべての国の人口（単位は100万人）を年に対してプロットしてください。 どの国がどれかを識別する必要はありません。

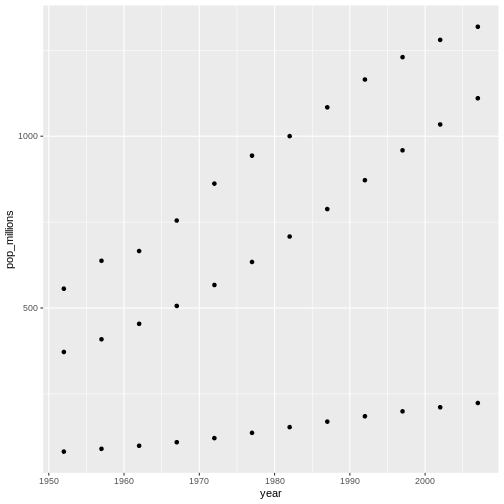
次に、中国、インド、インドネシアに対してのみグラフ化を行ってください。 こちらもどの国がどれかを識別する必要はありません。

人口（単位は100万人）を年に対してプロットして、プロットスキルをリフレッシュしましょう。

R 

ggplot(gapminder, aes(x = year, y = pop_millions)) +
 geom_point()
中国、インド、インドネシアの人口（単位は100万人）を年に対してプロットした散布図。国はラベル付けされていません。

R 

countryset <- c("China","India","Indonesia")
ggplot(gapminder[gapminder$country %in% countryset,],
       aes(x = year, y = pop_millions)) +
  geom_point()
中国、インド、インドネシアの人口（単位は100万人）を年に対してプロットした散布図。国はラベル付けされていません。

比較演算子、論理演算子、多くの関数もまたベクトル化されています：

比較演算子

R 

x > 2

出力 

[1] FALSE FALSE  TRUE  TRUE

論理演算子

R 

a <- x > 3  # または、明確にするために a <- (x > 3)
a

出力 

[1] FALSE FALSE FALSE  TRUE

ヒント：論理ベクトルの便利な関数

any() はベクトル内に1つでも TRUE が含まれていれば TRUE を返します。
all() はベクトル内のすべての要素が TRUE の場合にのみ TRUE を返します。

ほとんどの関数はベクトルに対して要素ごとに操作を行います：

関数

R 

x <- 1:4
log(x)

出力 

[1] 0.0000000 0.6931472 1.0986123 1.3862944

ベクトル化された操作は行列の要素ごとにも動作します：

R 

m <- matrix(1:12, nrow=3, ncol=4)
m * -1

出力 

     [,1] [,2] [,3] [,4]
[1,]   -1   -4   -7  -10
[2,]   -2   -5   -8  -11
[3,]   -3   -6   -9  -12

ヒント：要素ごとの積と行列積の違い

重要：* 演算子は要素ごとの積を行います！ 行列積を行うには、%*% 演算子を使用する必要があります：

R 

m %*% matrix(1, nrow=4, ncol=1)

出力 

     [,1]
[1,]   22
[2,]   26
[3,]   30

R 

matrix(1:4, nrow=1) %*% matrix(1:4, ncol=1)

出力 

     [,1]
[1,]   30

行列代数についての詳細は、Quick-R のリファレンスガイド を参照してください。

チャレンジ 3

次の行列を使用して：

R 

m <- matrix(1:12, nrow=3, ncol=4)
m

出力 

     [,1] [,2] [,3] [,4]
[1,]    1    4    7   10
[2,]    2    5    8   11
[3,]    3    6    9   12

以下を実行するとどうなるか予想してください：

  1. m ^ -1
  2. m * c(1, 0, -1)
  3. m > c(0, 20)
  4. m * c(1, 0, -1, 2)

出力が予想と違った場合は、ヘルパーに尋ねてください！

次の行列を使用して：

R 

m <- matrix(1:12, nrow=3, ncol=4)
m

出力 

     [,1] [,2] [,3] [,4]
[1,]    1    4    7   10
[2,]    2    5    8   11
[3,]    3    6    9   12

以下を実行するとどうなるか予想してください：

  1. m ^ -1

出力 

          [,1]      [,2]      [,3]       [,4]
[1,] 1.0000000 0.2500000 0.1428571 0.10000000
[2,] 0.5000000 0.2000000 0.1250000 0.09090909
[3,] 0.3333333 0.1666667 0.1111111 0.08333333
  1. m * c(1, 0, -1)

出力 

     [,1] [,2] [,3] [,4]
[1,]    1    4    7   10
[2,]    0    0    0    0
[3,]   -3   -6   -9  -12
  1. m > c(0, 20)

出力 

      [,1]  [,2]  [,3]  [,4]
[1,]  TRUE FALSE  TRUE FALSE
[2,] FALSE  TRUE FALSE  TRUE
[3,]  TRUE FALSE  TRUE FALSE

チャレンジ 4

次の分数列の合計を計算したいとします：

R 

 x = 1/(1^2) + 1/(2^2) + 1/(3^2) + ... + 1/(n^2)

これを手で書き出すのは面倒で、高い値の n に対しては不可能です。 ベクトル化を使用して、n=100 の場合の x を計算してください。 n=10,000 の場合の合計はどうなりますか？

次の分数列の合計を計算したいとします：

R 

 x = 1/(1^2) + 1/(2^2) + 1/(3^2) + ... + 1/(n^2)

これを手で書き出すのは面倒で、高い値の n に対しては不可能です。 ベクトル化を使用して、n=100 の場合の x を計算してください。 n=10,000 の場合はどうでしょうか？

R 

sum(1/(1:100)^2)

出力 

[1] 1.634984

R 

sum(1/(1:1e04)^2)

出力 

[1] 1.644834

R 

n <- 10000
sum(1/(1:n)^2)

出力 

[1] 1.644834

同じ結果を関数を使用して得ることもできます：

R 

inverse_sum_of_squares <- function(n) {
  sum(1/(1:n)^2)
}
inverse_sum_of_squares(100)

出力 

[1] 1.634984

R 

inverse_sum_of_squares(10000)

出力 

[1] 1.644834

R 

n <- 10000
inverse_sum_of_squares(n)

出力 

[1] 1.644834

ヒント：長さが異なるベクトルに対する操作

長さが異なるベクトルに対しても操作を実行できます。 これはリサイクルと呼ばれるプロセスを通じて行われます。 このプロセスでは、小さいベクトルが自動的に繰り返されて大きいベクトルの長さに一致します。 大きいベクトルが小さいベクトルの倍数ではない場合、Rは警告を出します。

R 

x <- c(1, 2, 3)
y <- c(1, 2, 3, 4, 5, 6, 7)
x + y

警告 

Warning in x + y: longer object length is not a multiple of shorter object
length

出力 

[1] 2 4 6 5 7 9 8

ベクトル x はベクトル y の長さに一致するようにリサイクルされました：

R 

x:  1  2  3  1  2  3  1
    +  +  +  +  +  +  +
y:  1  2  3  4  5  6  7
-----------------------
    2  4  6  5  7  9  8

まとめ

  • ループの代わりにベクトル化された操作を使用する。