ベクトル化

最終更新日：2024-10-12 | ページの編集

所要時間： 25分

概要

質問

  • How can I operate on all the elements of a vector at once?

目的

  • To understand vectorized operations in R.

Rの関数はほとんどがベクトル化されており、関数はベクトルの全ての要素を最初から操作してくれるので、ベクトルの要素ごとにいちいちループする必要がありません。 おかげで簡潔で読み易く、エラーの少ないコードを書くことができます。

R 

x <- 1:4
x * 2

出力 

[1] 2 4 6 8

積はベクトルの要素ごとに実行されました。

2つのベクトルを足し合わせることもできます:

R 

y <- 6:9
x + y

出力 

[1]  7  9 11 13

この場合 x の各要素が対応する yの要素に足されます。

R 

x:  1  2  3  4
    +  +  +  +
y:  6  7  8  9
---------------
    7  9 11 13

Here is how we would add two vectors together using a for loop:

R 

output_vector <- c()
for (i in 1:4) {
  output_vector[i] <- x[i] + y[i]
}
output_vector

出力 

[1]  7  9 11 13

Compare this to the output using vectorised operations.

R 

sum_xy <- x + y
sum_xy

出力 

[1]  7  9 11 13

チャレンジ１

gapminder データセットの pop 列でこれに挑戦してみましょう。

gapminder データフレームに百万人単位の人口を示す列を追加しましょう。 データフレームの先頭か最後を確認して、追加に成功したか確認しましょう。

gapminder データセットの pop 列でこれに挑戦してみましょう。

gapminder データフレームに百万人単位の人口を示す列を追加しましょう。 データフレームの先頭か最後を確認して、追加に成功したか確認しましょう。

R 

gapminder$pop_millions <- gapminder$pop / 1e6
head(gapminder)

出力 

      country year      pop continent lifeExp gdpPercap pop_millions
1 Afghanistan 1952  8425333      Asia  28.801  779.4453     8.425333
2 Afghanistan 1957  9240934      Asia  30.332  820.8530     9.240934
3 Afghanistan 1962 10267083      Asia  31.997  853.1007    10.267083
4 Afghanistan 1967 11537966      Asia  34.020  836.1971    11.537966
5 Afghanistan 1972 13079460      Asia  36.088  739.9811    13.079460
6 Afghanistan 1977 14880372      Asia  38.438  786.1134    14.880372

チャレンジ２

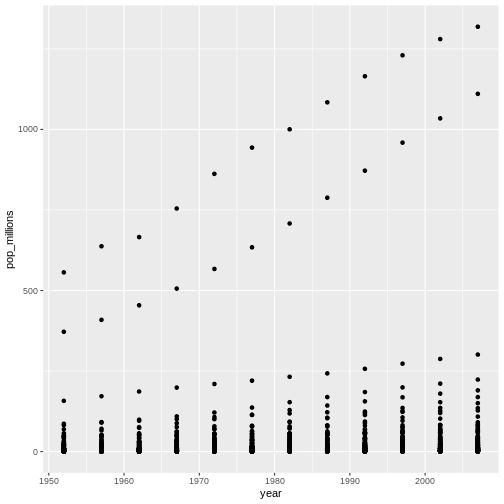
一つの図に、100万人単位の人口を年ごとにプロットしてみましょう。 国ごとの区別はつかなくていいです。

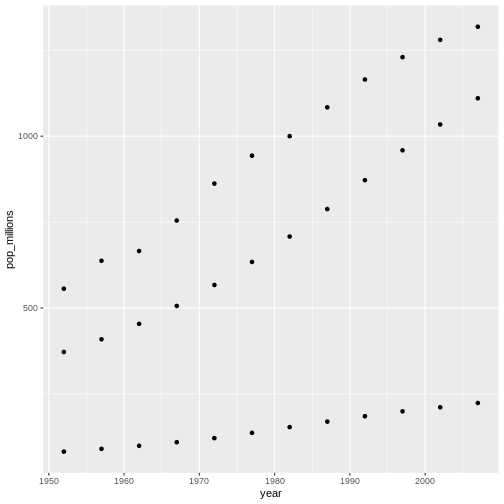
練習を繰り返して、中国とインドとインドネシアだけを含む図を 作ってみましょう。 先程と同じく、国ごとの区別はつかなくていいです。

チャレンジの解答 100万人単位の人口を年ごとにプロットして、作図方法を復習しましょう。

R 

ggplot(gapminder, aes(x = year, y = pop_millions)) +
 geom_point()
Scatter plot showing populations in the millions against the year for China, India, and Indonesia, countries are not labeled.

R 

countryset <- c("China","India","Indonesia")
ggplot(gapminder[gapminder$country %in% countryset,],
       aes(x = year, y = pop_millions)) +
  geom_point()
Scatter plot showing populations in the millions against the year for China, India, and Indonesia, countries are not labeled.

比較演算子や論理演算子に加え、多くの関数もベクトル化されています。

比較演算子

R 

x > 2

出力 

[1] FALSE FALSE  TRUE  TRUE

論理演算子

R 

a <- x 3 # より明確な書き方は a <- (x 3) a

エラー 

Error in parse(text = input): <text>:1:8: unexpected numeric constant
1: a <- x 3
           ^

Tip: 論理ベクトルに使える便利な関数

  • any() はベクトルの要素の中に一つでも TRUE があれば TRUE を返します。
  • all() はベクトルの要素が 全て TRUE であれば TRUE を返します。

ほとんどの関数はベクトルを要素ごとに処理します。

関数

R 

x <- 1:4
log(x)

出力 

[1] 0.0000000 0.6931472 1.0986123 1.3862944

ベクトル化された操作は行列を要素ごとに処理します:

R 

m <- matrix(1:12, nrow=3, ncol=4)
m * -1

出力 

     [,1] [,2] [,3] [,4]
[1,]   -1   -4   -7  -10
[2,]   -2   -5   -8  -11
[3,]   -3   -6   -9  -12

Tip: 要素ごとの積 vs. 行列の積

非常に重要: 演算子は要素ごとの積を行います！ To do matrix multiplication, we need to use the %*% operator:

R 

m %*% matrix(1, nrow=4, ncol=1)

出力 

     [,1]
[1,]   22
[2,]   26
[3,]   30

R 

matrix(1:4, nrow=1) %*% matrix(1:4, ncol=1)

出力 

     [,1]
[1,]   30

更に行列代数について知るには Quick-R reference guide を参照して下さい

チャレンジ３

以下のリストがあるとします：

R 

m <- matrix(1:12, nrow=3, ncol=4)
m

出力 

     [,1] [,2] [,3] [,4]
[1,]    1    4    7   10
[2,]    2    5    8   11
[3,]    3    6    9   12

Write down what you think will happen when you run:

  1. m ^ -1
  2. m * c(1, 0, -1)
  3. m > c(0, 20)
  4. m * c(1, 0, -1, 2)

Did you get the output you expected? If not, ask a helper!

以下のリストがあるとします：

R 

m <- matrix(1:12, nrow=3, ncol=4)
m

出力 

     [,1] [,2] [,3] [,4]
[1,]    1    4    7   10
[2,]    2    5    8   11
[3,]    3    6    9   12

Write down what you think will happen when you run:

  1. m ^ -1

出力 

          [,1]      [,2]      [,3]       [,4]
[1,] 1.0000000 0.2500000 0.1428571 0.10000000
[2,] 0.5000000 0.2000000 0.1250000 0.09090909
[3,] 0.3333333 0.1666667 0.1111111 0.08333333
  1. m * c(1, 0, -1)

出力 

     [,1] [,2] [,3] [,4]
[1,]    1    4    7   10
[2,]    0    0    0    0
[3,]   -3   -6   -9  -12
  1. m > c(0, 20)

出力 

      [,1]  [,2]  [,3]  [,4]
[1,]  TRUE FALSE  TRUE FALSE
[2,] FALSE  TRUE FALSE  TRUE
[3,]  TRUE FALSE  TRUE FALSE

チャレンジ４

以下の分数の数列の総和が知りたいとします: ~~~ x:

R 

 x = 1/(1^2) + 1/(2^2) + 1/(3^2) + ... + 1/(n^2)
  • /(n^) ~~~ これをタイプするのは面倒な上に、nが大きいと不可能です。 ベクトル化を用いて n = 100 の場合を計算しましょう。 n = 10,000 の時の総和はいくつでしょうか？

以下の分数の数列の総和が知りたいとします: ~~~ x:

R 

 x = 1/(1^2) + 1/(2^2) + 1/(3^2) + ... + 1/(n^2)
  • /(n^) ~~~ これをタイプするのは面倒な上に、nが大きいと不可能です。 ベクトル化を用いて n = 100 の場合を計算しましょう。 n = 10,000 の時の総和はいくつでしょうか？

R 

sum(1/(1:100)^2)

出力 

[1] 1.634984

R 

sum(1/(1:1e04)^2)

出力 

[1] 1.644834

R 

n <- 10000
sum(1/(1:n)^2)

出力 

[1] 1.644834

We can also obtain the same results using a function:

R 

inverse_sum_of_squares <- function(n) {
  sum(1/(1:n)^2)
}
inverse_sum_of_squares(100)

出力 

[1] 1.634984

R 

inverse_sum_of_squares(10000)

出力 

[1] 1.644834

R 

n <- 10000
inverse_sum_of_squares(n)

出力 

[1] 1.644834

Tip: Operations on vectors of unequal length

Operations can also be performed on vectors of unequal length, through a process known as recycling. This process automatically repeats the smaller vector until it matches the length of the larger vector. R will provide a warning if the larger vector is not a multiple of the smaller vector.

R 

x <- c(1, 2, 3)
y <- c(1, 2, 3, 4, 5, 6, 7)
x + y

警告 

Warning in x + y: longer object length is not a multiple of shorter object
length

出力 

[1] 2 4 6 5 7 9 8

Vector x was recycled to match the length of vector y

R 

x:  1  2  3  1  2  3  1
    +  +  +  +  +  +  +
y:  1  2  3  4  5  6  7
-----------------------
    2  4  6  5  7  9  8

まとめ

  • Use vectorized operations instead of loops.